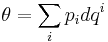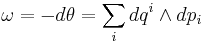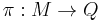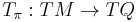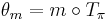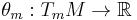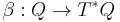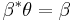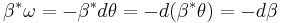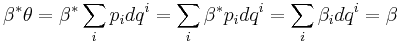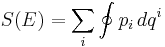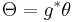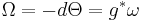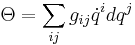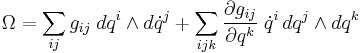Tautological one-form
In mathematics, the tautological one-form is a special 1-form defined on the cotangent bundle T*Q of a manifold Q. The exterior derivative of this form defines a symplectic form giving T*Q the structure of a symplectic manifold. The tautological one-form plays an important role in relating the formalism of Hamiltonian mechanics and Lagrangian mechanics. The tautological one-form is sometimes also called the Liouville one-form, the Poincaré one-form, the canonical one-form, or the symplectic potential. A similar object is the canonical vector field on the tangent bundle.
In canonical coordinates, the tautological one-form is given by
Equivalently, any coordinates on phase space which preserve this structure for the canonical one-form, up to a total differential (exact form), may be called canonical coordinates; transformations between different canonical coordinate systems are known as canonical transformations.
The canonical symplectic form is given by
Contents |
Coordinate-free definition
The tautological 1-form can also be defined rather abstractly as a form on phase space. Let  be a manifold and
be a manifold and 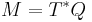 be the cotangent bundle or phase space. Let
be the cotangent bundle or phase space. Let
be the canonical fiber bundle projection, and let
be the induced tangent map. Let m be a point on M, however, since M is the cotangent bundle, we can understand m to be a map of the tangent space at 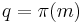 :
:
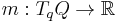 .
.
That is, we have that m is in the fiber of q. The tautological one-form 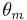 at point m is then defined to be
at point m is then defined to be
It is a linear map
and so
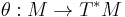 .
.
Properties
The tautological one-form is the unique horizontal one-form that "cancels" a pullback. That is, let
be any 1-form on Q, and 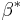 be its pullback. Then
be its pullback. Then
so that, by the commutation between the pull-back and the exterior derivative:
This can be most easily understood in terms of coordinates:
Action
If H is a Hamiltonian on the cotangent bundle and 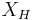 is its Hamiltonian flow, then the corresponding action S is given by
is its Hamiltonian flow, then the corresponding action S is given by
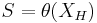 .
.
In more prosaic terms, the Hamiltonian flow represents the classical trajectory of a mechanical system obeying the Hamilton-Jacobi equations of motion. The Hamiltonian flow is the integral of the Hamiltonian vector field, and so one writes, using traditional notation for action-angle variables:
with the integral understood to be taken over the manifold defined by holding the energy  constant:
constant: 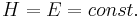 .
.
On metric spaces
If the manifold Q has a Riemannian or pseudo-Riemannian metric g, then corresponding definitions can be made in terms of generalized coordinates. Specifically, if we take the metric to be a map
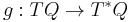 ,
,
then define
and
In generalized coordinates 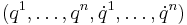 on TQ, one has
on TQ, one has
and
The metric allows one to define a unit-radius sphere in 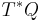 . The canonical one-form restricted to this sphere forms a contact structure; the contact structure may be used to generate the geodesic flow for this metric.
. The canonical one-form restricted to this sphere forms a contact structure; the contact structure may be used to generate the geodesic flow for this metric.
See also
References
- Ralph Abraham and Jarrold E. Marsden, Foundations of Mechanics, (1978) Benjamin-Cummings, London ISBN 0-8053-0102-X See section 3.2.